多目标规划法
1.多目标规划法概述
多目标规划法也是运筹学中的一个重要分支,它是在线性规划的基础上,为解决多目标决策问题而发展起来的一种科学管理的数学方法
多目标规划的概念是 1961年由美国数学家查尔斯和库柏首先提出的。
多目标规划是指标准型为:
minZ=CY
s.t AX+Y—Y + = b
X,Y,Y − Y + 1�0
的规划问题。这里 C、Y、A、X、Y-、Y + 、b均为矩阵或向量的形式。
2.多目标规划标准型的特点
与线性规划相比,多目标规划标准型的特点在于:
1、偏差列向量 Y − 、Y + 。Y − 、Y + 分别为负、正偏差列向量,各有 m个元素 Y − 、y + 。…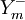 与
与 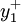
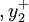 ,…,
,…,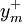 (m是约束方程的个数)。负偏差变量的经济含义为当实际值小于目标值时,实际值与目标值的偏差为负偏差,正偏差变量的经济含义与之恰恰相反。
(m是约束方程的个数)。负偏差变量的经济含义为当实际值小于目标值时,实际值与目标值的偏差为负偏差,正偏差变量的经济含义与之恰恰相反。
2、价值系数行向量c。c的元素最多不超过 2m个,由目标优先权等级 Pi和目标优先权系数η组成,即 c = (c1,c2…,c2m)=(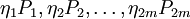 ),在多目标规划的目标函数中,出现的变量只能是偏差变量。也就是说,列向量 y以正偏差变量和负偏差变量为元素。目标优先权等级 Pi既不是变量,也不是常数,它只是说明不同目标实现的先后顺序,这种优先等级的确定一般是由企业决策部门根据企业具体情况及各目标的轻重缓急加以确定的。而目标优先级系数,则说明同一优先级目标相互之间的比例关系。
),在多目标规划的目标函数中,出现的变量只能是偏差变量。也就是说,列向量 y以正偏差变量和负偏差变量为元素。目标优先权等级 Pi既不是变量,也不是常数,它只是说明不同目标实现的先后顺序,这种优先等级的确定一般是由企业决策部门根据企业具体情况及各目标的轻重缓急加以确定的。而目标优先级系数,则说明同一优先级目标相互之间的比例关系。
3.多目标规划法的基本解法
多目标规划的解法主要有单纯形法和图解法。图解法一般只适用于两个决策变量的情形。单纯形法对于求解多目标规划有普遍意义。
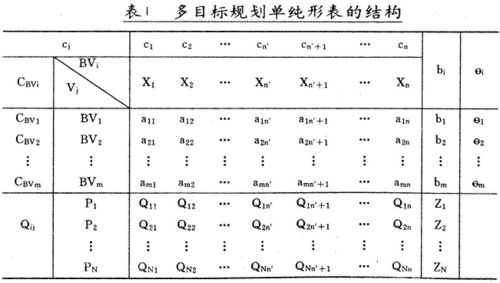
多目标规划单纯形表的结构如表1。
表中 Vj———变量,X1,X2,…,Xn是决策变量,其余 n-n'个是偏差变量;
Cj———价值系数,因多目标规划目标函数不包含决策变量,所以 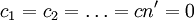 ;
;
bi———目标约束常数;
θi———θ判据;
BVi———基变量名;
CBVi———基变量价值系数;
aij———作业系数;
Qij———单纯形判据矩阵元素;
Pj———目标优先权排序;
Zj———第 j个优先级目标的目标函数值。
表1与线性规划单纯形表相比,最大的不同是单纯形判据是一个 N×n矩阵,而不是列向量,且有 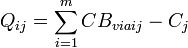 。
。
目标优先权排序 P1,P2,…,PN给出了单纯形迭代过程中实现目标的顺序。在实现某一优先级目标后,应依顺序考虑一个优先级能否实现。但是,不能为实现较低目标而使较高级目标的实现受到影响。
4.多目标规划的主要应用领域
多目标规划的概念是 1961年由美国数学家查尔斯和库柏首先提出的。至今有些理论问题尚在探讨之中,应用范围还不如线性规划广泛。在资源分配、计划编制、生产调度等方面有一定的’应用。但是,作为一种决策方法,多目标规划的应用前景还是很乐观的。企业决策者掌握和运用这种方法将有助于提高管理和决策水平。
5.多目标规划的案例分析
案例一:纺织厂的多目标规划
某纺织厂生产窗帘布和衣料两种布料,该厂对这两种布料的生产能力均是 1000m/h,工厂正常生产能力每周 80h,根据市场预测,下周最大销售量窗帘布70000m、衣料45000m,窗帘布每米获利 2.50元,衣料每料获利 1.50元。该厂定出的经营目标是:
P1:保证生产均衡稳定,避免开工不足;
P2:每周加班时间不超过10h;
P3:努力实现最大销售量;
P4:尽可能减少加班时间。
本案例多目标规划模型的决策变量为;x1———周内窗帘布生产的小时数;x2———周内衣料生产的小时数。
每周正常生产能力约束:
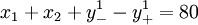
式中 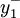 和
和 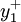 分别表示每周开工低于正常生产能力的负偏差及超出正常生产能力的正偏差。
分别表示每周开工低于正常生产能力的负偏差及超出正常生产能力的正偏差。
销售目标约束:
x1 + y2 − = 70000 / 1000 = 70
x2 + y3 − = 45000 / 1000 = 45
因产量不能超过最大销售量,所以 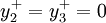
加班时间限制目标约束:
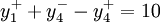
式中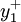 取自每周正常生产能力约束的正偏差,即加班小时数,
取自每周正常生产能力约束的正偏差,即加班小时数,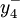 与
与 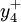 分别表示加班时间不足 10h的负偏差和超过10h的正偏差。
分别表示加班时间不足 10h的负偏差和超过10h的正偏差。
案例二:用多目标规划法优化企业资本结构[1]
多目标规划法是运筹学中的数学规划方法之一。
它是在运筹学基本的数学规划方法——线性规划法的基础上,为了克服线性规划方法目标函数单一、约束条件苛刻、无法解决矛盾条件下的规划问题等缺点而发展起来的规划方法,使用这种模型能够解决多种目标同时存在的规划问题。它以求解实际结果与目标或资源限制之间的偏差变量最小作为目标函数构造的出发点,解决企业生产经营中的各种目标的平衡问题,而被较为广泛地应用。把目标规划方法引入资本结构的决策之中,力图使该决策在考虑企业多个影响因素的条件下进行,也使得决策结果更符合客观实际。
1.资本结构的多目标规划模型
多目标规划法的基本数学模型为:
目标函数:
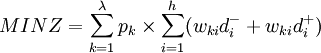
约束条件:
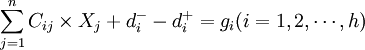
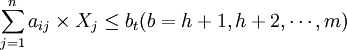
或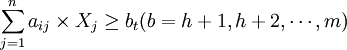
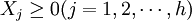
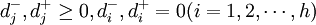
式中:Xj——决策变量;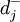 、
、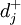 ——正负偏差变量;Cij——第i项目约束条件中Xj的系数;aij——第t项资源约束条件中Xj的系数;一般为各项资源的单位消耗定额;gi——第i项目标的既定值;bt——第t项资源约束条件的限制值;Pk——目标的优先级别;
——正负偏差变量;Cij——第i项目约束条件中Xj的系数;aij——第t项资源约束条件中Xj的系数;一般为各项资源的单位消耗定额;gi——第i项目标的既定值;bt——第t项资源约束条件的限制值;Pk——目标的优先级别;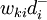 、
、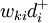 ——第k级优先级目标中
——第k级优先级目标中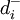 、
、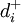 的加权系数。
的加权系数。
由于企业资本结构包括资本中的项目构成和各种比例构成,因此,可以将企业的资产负债率和权益与资产总额的比率设为模型中的两个基本变量vj、vz。再根据涉及企业资本结构的各项指标进行各约束条件的设置。
2.资本结构的多目标规划模型的约束条件设置
企业的经营是在一个非常复杂的大系统中进行的,许多不确定性因素干扰着企业的经济效益。但是,从影响资本结构决策的角度看,则主要有资金成本、自有资金收益率、企业资本保值增值率、经营风险、获利能力等因素的影响,因此,其约束环境设置时也主要应考虑以下几个方面:
1)企业预期的资本构成
按照企业资本构成的基本公式:资产=负债+所有者权益,设置出运算的负债总额与自资本总额之和等于企业预期的资产总额的约束。为便于运算,又将其设置为资产负债率和权益与资产总额的比率之和等于1。
2)资金成本与自有资金收益率之间相互消长的关系
根据财务杠杆原理,自有资金收益率的大小取决于企业的投资收益率,也取决于资金成本的大小。因此,模型中可设置出在一定的资金成本前提下的自有资金收益率,并使其大于或等于某一期望值的约束条件。
3)考虑资本结构给企业经营带来的风险因素
一般认为,企业的期望收益越大则风险越大。模型中此项约束方程的设置应视不同行业的企业设置风险界限,将风险控制在一定的范围之内。
4)合理的资本结构应使资本的保值增值率大于或等于一定的标准
为保护所有者的利益,财务制度规定企业的资本必须按一定的比率保值增值,在进行资本结构决策时,应结合盈利水平考虑此因素并以一定的下限设置约束。
5)企业的获利能力尽可能达到行业的水平
企业的获利能力有许多的表示方法,已获息倍数是其中一个重要的指标,它从盈利与利息之间倍数关系的一定角度上反映了企业的盈利水平。因此,可以某一定值作下限设置出一个约束条件。
根据这些约束条件,建立相应的数学模型,上机求解,即可求出最佳的负债额和资产负债率。
3.模型应用
某企业的市场环境不好,经营状况也不好,总资产报酬率仅为2.08%,平均负债利息率为3.6%。企业现有资产总额为8696.3万元,本期期望收益额为78万元。在此前提下,用多目标规划法确定该企业合理的资本结构。
1)约束条件设置
第1级目标:
根据资产的结构,设资产负债率vj和权益与资产总额的比率vz之和等于1。
即: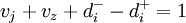 ;
;
第2级目标:
在现有的经营状态下,若企业能保持78万元的盈利,则企业的净资产收益率r不小于0.77%。
即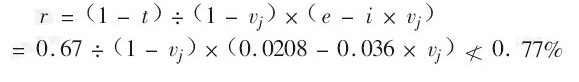
式中:e为总资产报酬率
整理得: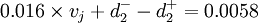 ;
;
第3级目标:
根据企业的盈利能力及经营条件。
企业实现总资产期望报酬率过程中的风险不大于0.1,用标准差F(e)来表示风险。
![F(e)=left[sum^n_{t=1}(e_i-e^t)^2times P_i right]^{frac{1}{2}}](http://wiki.mbalib.com/w/images/math/d/9/f/d9f8300abcfca0009011076b0c328d70.png)
根据自有资金收益率与总资产报酬率之间的关系,推导出实现自资金收益率r与风险的关系式,并根据实际情况令其不大于10%。
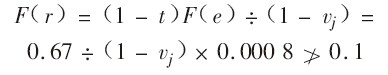
整理得: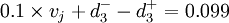 ;
;
第4级目标:
根据财务制度的规定,令资本保值增值率大于105%
因为:![left[Ktimes v_z+Mtimes(1-d)right]div K times v_z times 100%>105%](http://wiki.mbalib.com/w/images/math/7/e/0/7e0b499c939c86a4e825218c62ca6428.png)
即:![left[Ktimes v_z+Mtimes(1-d)iright]div K times(1-v_j)times 100%>105%](http://wiki.mbalib.com/w/images/math/7/2/8/728a0539ceacf526f817acae193114be.png)
整理得: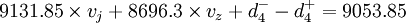
式中:K——企业资产总额;M——企业计划期的期望收益额。
第5级目标:
企业的已获息倍数不小于几年行业的平均水平1.4
因为: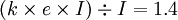
整理得: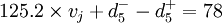
2)构造目标函数根据各约束方程中主要指标的性质,构建出最优资本结构的目标函数模型为:。
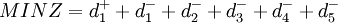
3)上机运算,得到如下结果。
vj = 0.58904 = 59.04%
vz = 0.4096 = 40.96%
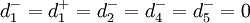 ;
;
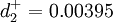
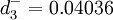
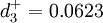
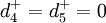
4.结论
该企业在考虑各种条件后的资产负债率vj应为59.04%,所有者权益与资产的比率vz应为40.96%。即59%负债和41%所有者权益构成企业合理的资本结构。
