相关表
1.什么是相关表
相关表是一种显示变量之间相关关系的统计表。通常将两个变量的对应值平行排列,且其中某一变量按其取值大小顺序排列,便可得到相关表。
如下表(某商店10名售货员的工龄和日工资的相关系表):
| 工龄(年) | 4 | 4 | 5 | 6 | 7 | 8 | 8 | 9 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 日工资(百元) | 42 | 46 | 50 | 60 | 64 | 68 | 74 | 72 | 80 | 84 |
2.相关表的类型
对现象总体两种相关的标志作相关分析,研究其相互依存关系,首先要通过对实际调查取得一系列成对的标志值资料,作为相关分析原始数据。根据资料是否分组,相关表可分为简单相关表和分组相关表。
1、简单相关表
简单相关表是资料未经分组的相关表,它是把因素标志值按照从小到大的顺序并配合结果标志值一一对应而平行排列起来的统计表。
简单相关表是现象标志之间相关研究初步结果的表现。表中X与Y两标志的标志值(变量值),如下表:
| x | x1 | x2 | … | xn |
| y | y1 | y2 | … | yn |
例如,为研究分析产量(件)和单位成本(元)的关系,设有30个同类企业调查得到的原始资料,如下表:
| 产量(件) | 20 | 30 | 20 | 20 | 40 | 30 | 40 | 80 | 80 | 50 | 40 | 30 | 20 | 80 | 50 |
| 单位成本(元) | 18 | 16 | 16 | 15 | 16 | 15 | 15 | 14 | 14 | 15 | 15 | 16 | 18 | 14 | 14 |
| 产量(件) | 20 | 50 | 20 | 30 | 50 | 20 | 50 | 40 | 20 | 80 | 40 | 20 | 50 | 80 | 30 |
| 单位成本(元) | 16 | 16 | 18 | 16 | 15 | 18 | 15 | 14 | 16 | 14 | 15 | 16 | 14 | 15 | 15 |
根据上述资料,编制如下简单相关表:
| 产量(件) | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 30 | 30 | 30 | 30 | 30 | 40 |
| 单位成本(元) | 15 | 16 | 16 | 16 | 16 | 18 | 18 | 18 | 18 | 15 | 15 | 15 | 16 | 16 | 14 |
| 产量(件) | 40 | 40 | 40 | 40 | 50 | 50 | 50 | 50 | 50 | 50 | 80 | 80 | 80 | 80 | 80 |
| 单位成本(元) | 15 | 15 | 15 | 16 | 14 | 14 | 15 | 15 | 15 | 16 | 14 | 14 | 14 | 14 | 15 |
从表中可以直观地发现,随着产量的增加,单位成本也有降低的趋势。尽管在同样产量的情况下,单位成本存在差异,但是仍然体现两者存在一定的依存关系。
2、分组相关表
1)单变量分组相关表
自变量分组并计算次数次数,而对应的因变量不分组,只计算其平均值。根据具体情况,可以是单项式,也可以是组距式。就上例,按产量分组而形成的单变量分组表如下:
| 产量(件)x | 企业数n | 平均单位成本(元)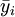 |
|---|---|---|
| 20 | 9 | 9 |
| 30 | 5 | 5 |
| 40 | 6 | 5 |
| 50 | 5 | 6 |
| 80 | 5 | 5 |
现象依存关系的分析,通常使用单变量分组相关表形式。
若将这种单变量分组相关表和简单相关表加以比较,不难发现单变量分组相关表使得资料简化,能够更清晰地反映出两变量的关系。从表上可以看出产量和单位成本之间存在着负相关的关系。
2)双变量分组相关表
双变量分组相关表,这是自变量和因变量都进行分组而成的相关表。这种表形似棋盘,故又称棋盘式相关表。
其编制程序是:首先,分别确定自变量和因变量的组数;其次按两个变量的组数设计棋盘式表格;最后,计算各组次数置于相对应的方格之中。仍以上例说明,编制的结果如下表:
| 单位成本(元/件) | 产量x(件) | 合计 | ||||
| 20 | 30 | 40 | 50 | 80 | ||
| 18 | 4 | 4 | ||||
| 16 | 4 | 3 | 1 | 9 | ||
| 15 | 1 | 2 | 3 | 3 | 1 | 10 |
| 14 | 1 | 2 | 4 | 7 | ||
| 合计 | 9 | 5 | 5 | 6 | 5 | 30 |
从表中看出,单位成本集中在左上角到右下角的斜线上。表示产量与单位成本是负相关。
在分组相关表中,自变量的每一个变量值都相应有一个因变量的统计分配数列,因变量的每一个变量值也必有一个相应的自变量统计分配数列。
| x1 = 20 | y1 = 14 | ||
| yx1 | fx1 | xy4 | fy4 |
| 18 | 4 | 40 | 1 |
| 16 | 3 | 50 | 2 |
| 15 | 1 | 80 | 4 |
这种分配数列表示当产量较低时(20件),相应有较多的企业单位成本较高(单位成本18的有4个,16的也有4个),而单位成本最小时(14元),其产量是比较多的企业(产量80占4个,50的占2个)。我们就是要从这一系列分配数列中来观察相关的方向:单位成本随着产量的增加而减少。
