随机误差
1.什么是随机误差[1]
随机误差也称为偶然误差和不定误差,是由于在测定过程中一系列有关因素微小的随机波动而形成的具有相互抵偿性的误差。
它的特点:大小和方向都不固定,也无法测量或校正。随机误差的性质是:随着测定次数的增加,正负误差可以相互低偿,误差的平均值将逐渐趋向于零。
2.随机误差的原因[1]
产生随机误差的原因有许多。例如,在测量过程中由于温度、湿度以及灰尘等的影响都可能引起数据的波动。再比如在读取滴定管数据时,估计的小数点后第二位的数值,几次读数不一致。这类误差在操作中不能完全避免。
随机误差的大小、正负在同一个实验室中不是恒定的,并很难找到产生的确切原因,所以又称不定误差。
3.随机误差的规律性
从表面上看,它的出现似乎没有规律,即在单次测定过程中,其大小及符号无法预言,没有任何规律性,具有非单向性的特点。但是,如果进行反复多次测定,就会发现随机误差的出现还是有一定的规律的,即具有统计规律性。总的来说,大小相等的正、负误差出现的几率相等,小误差出现的机会多,大误差出现的机会少,特大的正、负误差出现的机会更小。这一规律可以用正态分布曲线(图1)表示。[1]
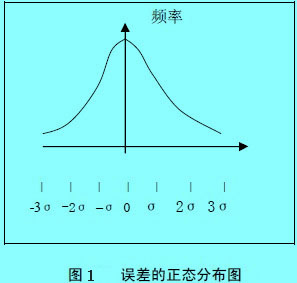
图中横轴代表误差的大小,以总体标准差σ为单位,纵轴代表误差发生的频率。
随机误差是由随机因素引起的,可大可小,可正可负,粗看起来,无规律可循,但经过大量实验可以发现,随机误差的分布也有一定规律性:
1、大小相近的正误差和负误差出现的机率相等,即绝对值相近 ( 或相等 ) 而符号相反的误差以同等的机率出现。
2、小误差出现的频率高,而大误差出现的频数较低,很大误差出现的机率近于零或极少。即:偶然误差的规律符合正态分布。在消除系统误差的情况下,增加测定次数,取其平均值,可减少偶然误差。实际工作中测定次数为4~6次已经足够了。一般情况下,很少有超过4次平行测定的。
4.随机误差的注意点[1]
应该指出的是,系统误差与随机误差的划分也不是绝对的,有时很难区分某种误差是系统误差还是随机误差。例如判断滴定终点的迟早、观察颜色的深浅,总有一定的随机性。
另外,有些因素在短时间内引起的误差可能属于随机误差,但在一个较长的时期内就可能转化为系统误差。例如,温度的影响,在某一天或几天时间内进行测量时,它的波动所引起的误差应属于随机误差,可是在某一季节较长时间内,它的影响所造成的误差就可以划为系统误差。
除此之外,不同的操作方法,误差的性质也有所不同。例如对于具有分刻度的吸量管,不同的吸量管误差可能是各不相同的。如果用几支吸量管吸取相同体积同一溶液,所产生的误差属于随机误差;如果只用一只吸量管,几次吸取相同体积的同一溶液,造成的误差则应属于系统误差;但是,如果每次吸取溶液时使用不同的刻度区,由于不同刻度区的误差可能有大有小,有正有负,这时产生的误差就转化为随机误差。
除了以上两类误差外,在测定过程中,由于操作者粗心大意或不按操作规程办事而造成的测定过程中溶液的溅失、加错试剂、看错刻度、记录错误,以及仪器测量参数设置错误等等,都属于过失误差,会对计量或测定结果带来严重影响,必须注意避免。为此,必须严格遵守操作规程,一丝不苟,耐心细致的进行实验,在学习过程中养成良好的实验习惯。
