洛伦兹曲线
1.洛伦兹曲线
洛伦兹曲线研究的是国民收入在国民之间的分配问题。为了研究国民收入在国民之间的分配问题,美国统计学家(或说奥地利统计学家)M.O.洛伦兹(Max Otto Lorenz,1903- )1907年(或说1905年)提出了著名的洛伦兹曲线。意大利经济学家基尼在此基础上定义了基尼系数。
2.洛伦兹曲线图示
画一个矩形,矩形的高衡量社会财富的百分比,将之分为五等份,每一等分为20的社会总财富。在矩形的长上,将100的家庭从最贫者到最富者自左向右排列,也分为5等分,第一个等份代表收入最低的20的家庭。在这个矩形中,将每一百分的家庭所有拥有的财富的百分比累计起来,并将相应的点画在图中,便得到了一条曲线就是洛伦兹曲线。
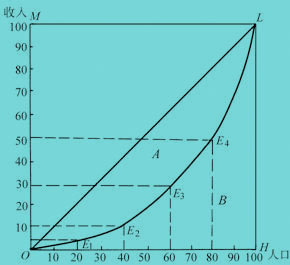
显而易见,洛伦兹曲线的弯曲程度具有重要意义。一般来说,它反映了收入分配的不平等程度。弯曲程度越大,收入分配程度越不平等;反之亦然。特别是,如果所有收入都集中在某一个人手中,而其余人口均一无所有,收入分配达到完全不平等,洛伦兹曲线成为折线OHL;另一方面,如果任一人口百分比等于其收入百分比,从而人口累计百分比等于收入累计百分比,则收入分配就是完全平等的,洛伦兹曲线成为通过原点的45度线OL。
3.洛伦兹曲线的作用
洛伦兹曲线用以比较和分析一个国家在不同时代或者不同国家在同一时代的财富不平等,该曲线作为一个总结收入和财富分配信息的便利的图形方法得到广泛应用。
图中横轴OH表示人口(按收入由低到高分组)的累积百分比,纵轴OM表示收入的累积百分比,弧线OL为洛伦兹曲线。
洛伦兹曲线的弯曲程度有重要意义。一般来讲,它反映了收入分配的不平等程度。弯曲程度越大,收入分配越不平等,反之亦然。特别是,如果所有收入都集中在一人手中,而其余人口均一无所获时,收入分配达到完全不平等,洛伦兹曲线成为折线OHL.另一方面,若任一人口百分比均等于其收入百分比,从而人口累计百分比等于收入累计百分比,则收入分配是完全平等的,洛伦兹曲线成为通过原点的45度线OL。
一般来说,一个国家的收入分配,既不是完全不平等,也不是完全平等,而是介于两者之间。相应的洛伦兹曲线,既不是折线OHL,也不是45度线OL,而是像图中这样向横轴突出的弧线OL,尽管突出的程度有所不同。
将洛伦兹曲线与45度线之间的部分A叫做“不平等面积”,当收入分配达到完全不平等时,洛伦兹曲线成为折线OHL,OHL与45度线之间的面积A+B叫做“完全不平等面积”。不平等面积与完全不平等面积之比,成为基尼系数,是衡量一国贫富差距的标准。基尼系数G=A/(A+B).显然,基尼系数不会大于1,也不会小于零。
4.洛伦兹曲线的方法[1]
尽管可根据收入分配的统计数据加以描绘,但至今却未能找到一种有效的方法,准确地拟合洛伦兹曲线方程并由此求出精确的基尼系数。目前常被使用的方法主要有三种:
(1)几何计算法。即根据分组资料,按几何图形分块近似逼近计算的方法。
(2)间接拟合法。即先拟合求出收入分配的概率密度函数,再根据概率密度函数导出洛伦兹曲线。
(3)曲线拟合法,即选择适当的曲线直接拟合洛伦兹曲线,常用的曲线有二次曲线、指数曲线和幂函数曲线。
利用第一种方法不能得到洛伦兹曲线的表达式,只能用来计算基尼系数,但由于在计算分块面积时用直线近似地代替曲线,所估计的基尼系数要小于实际值,尤其在数据点较少时,误差较大。第二种方法由于计算收入分配的概率密度的复杂性,很难提出合适的概率函数。至于第三种方法,即直接用曲线方程去拟合洛伦兹曲线,应该不失为一种较好的方法,但目前主要的问题在于现有常用的曲线并不适用,曲线含义不明确,或拟合误差较大。
为了更准确地描述洛伦兹曲线和精确地估计基尼系数,我们通过分析洛伦兹曲线的特性,设计出一条洛伦兹曲线方程,对洛伦兹曲线直接进行拟合。经过实例分析,拟合效果好,由洛伦兹曲线可推导出基尼系数的计算公式,计算结果精确度也很高。
